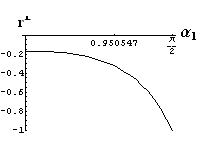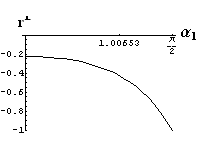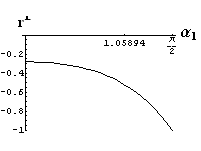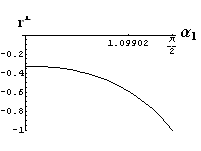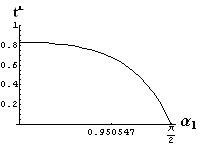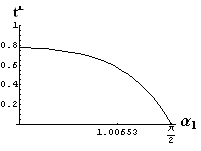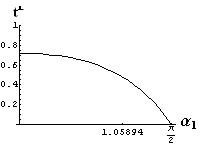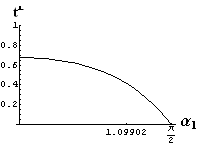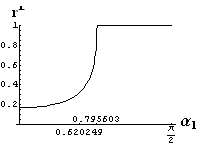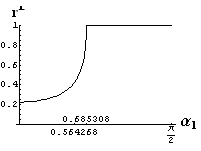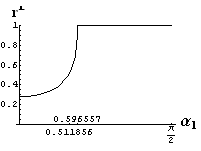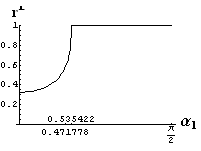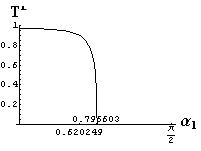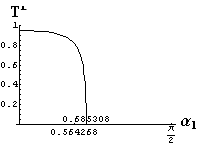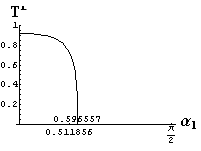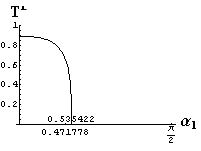Kurzy pro studenty
Mathematica a Mathematica CalcCenter ve výuce fyziky - materiály a vzorové příklady
Teorie elekromagnetického pole
i) pole elektrostatických multipólů
- řešení a znázornění polí elektrostatických multipólů, složených z bodových nábojů, s důrazem na axiální multipóly
- problém byl řešen dvojím způsobem:
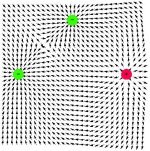
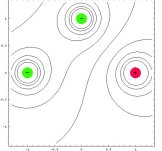
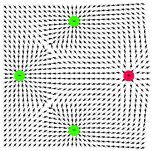
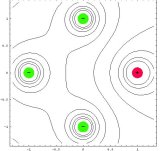
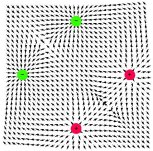
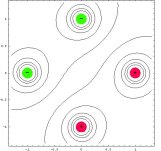
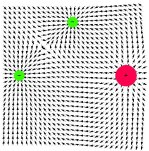
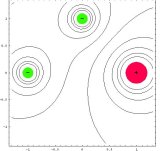
• s použitím standardních knihoven Mathematica byly vykreslovány ekvipotenciální hladiny v poli skalárního potenciálu a v rastru bodů znázorněny směry největšího poklesu v poli skalárního potenciálu, tedy směry vektoru elektrické intenzity. Toto řešení dává hrubou představu o průběhu siločar a je jednoduše aplikovatelné i pro složitější elektrostatické multipóly
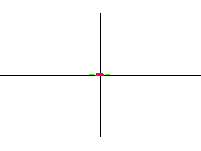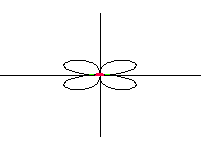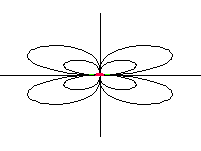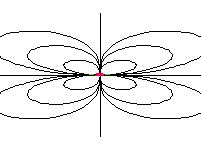
• druhý způsob řešení vycházel z řešení rovnice siločar a pomocí animací jsou jednotlivé siločáry postupně vykreslovány. Řešení je použitelné pouze tehdy, pokud je rovnice siločar řešitelná, tedy především pro axiální multipóly.
| dipól |  |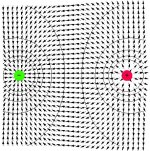
 |
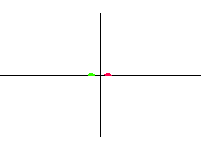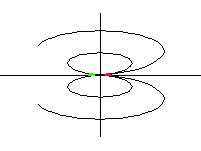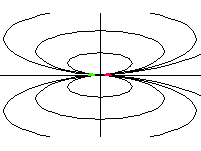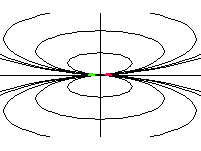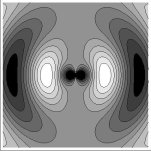
| kvadrupól axiální |  |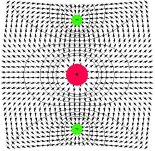
 |
| oktupól axiální |  |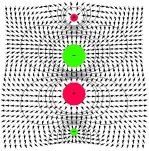
 |
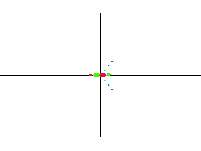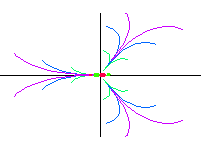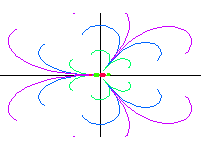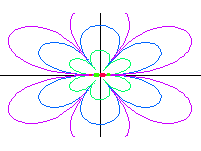obecné multipóly |
|
|
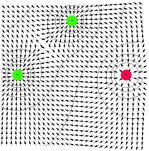
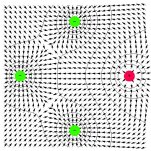
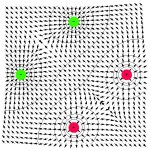
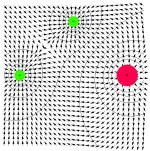
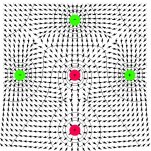
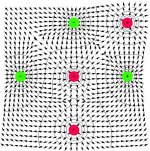
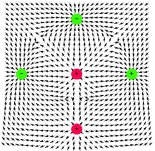
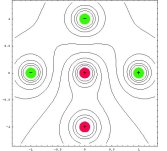
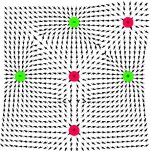
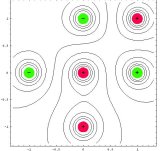
ii) magnetostatické pole permanentního magnetu
- znázornění magnetostatického pole permanentního magnetu pomocí indukčních čar
| permanentní magnet |  |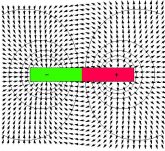
 |
iii) oscilující dipól
- znázornění elektrické složky nestacionárního elektromagnetického pole oscilujícího dipólu jako základního klasického zdroje nestacionárního elektromagnetického pole
- pomocí animací jsou postupně vykreslovány siločáry a znázorňováno jejich uzavření a další šíření pole ve formě elektrických vírů
oscilující dipól změna orientace vektoru elektrické intenzity je zde znázorněna změnou barvy vírů
|
 obrázek - dipole-oscilujici.jpg  obrázek - dipole-oscilujici2.jpg |
 animace - dipole-oscilujici.gif  animace - dipole-oscilujici2.gif |
iv) teorie šíření elektromagnetických vln v dielektrických anizotropních krystalech
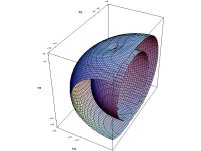
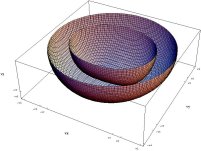
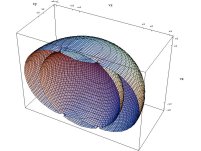
- znázornění plochy fázových rychlostí pro dvouosé krystaly pomocí 2D a 3D grafů
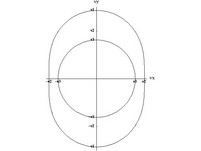
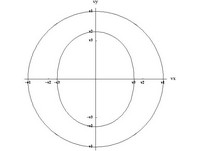
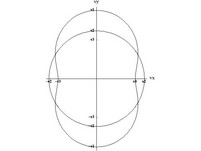
plochy fázových rychlostí 2D 3D |
2D
 obrázek - rezXYfazrych.jpg  obrázek - rezYZfazrych.jpg  obrázek - rezXZfazrych.jpg |
3D
 obrázek - plochafazrych3D.jpg  obrázek - plochafazrych3D3.jpg  obrázek - plochafazrych3D2.jpg |
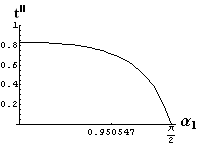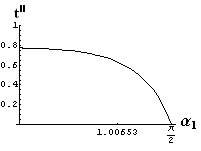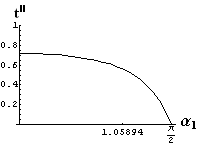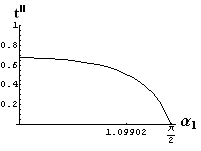
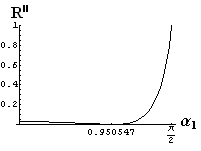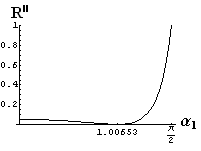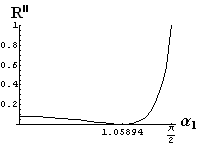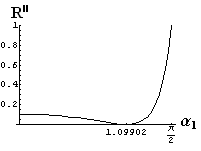
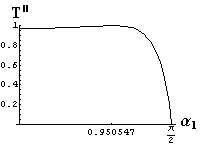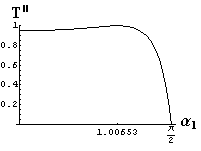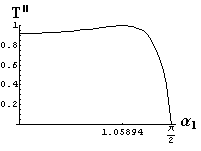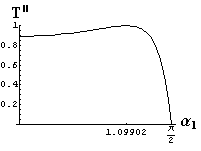
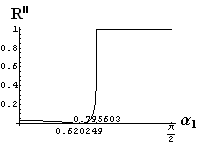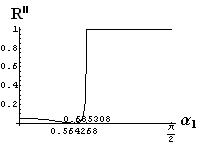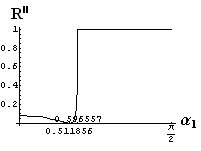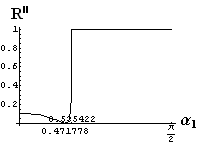
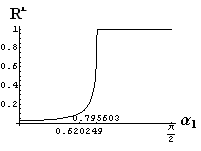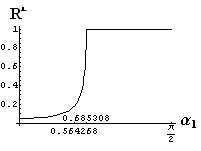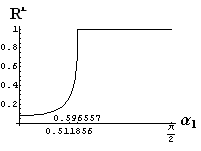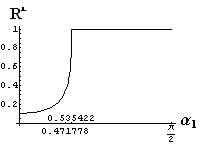
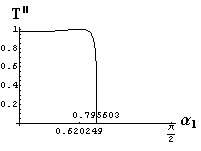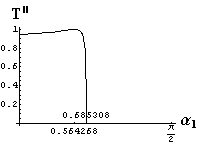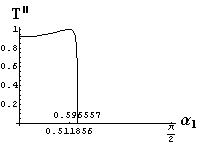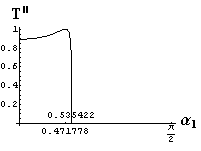
v) jevy na rozhraní dvou prostředí
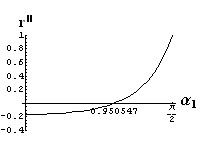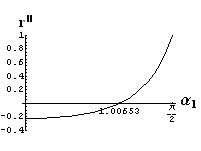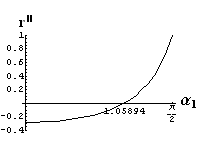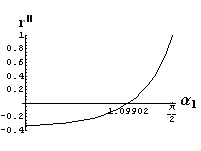
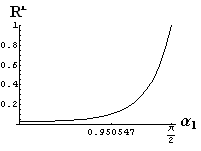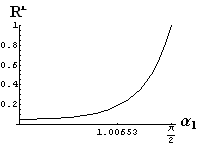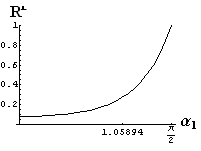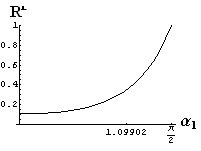
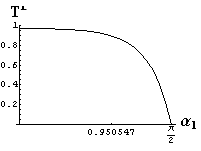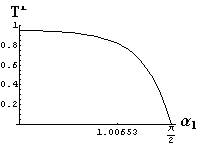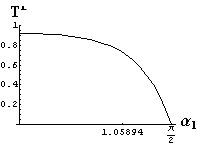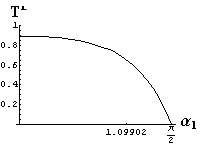
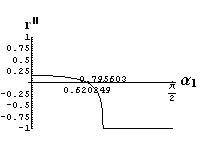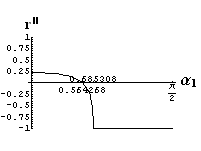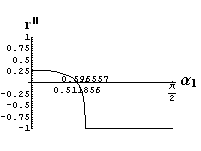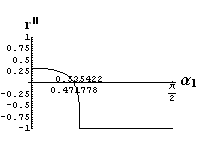
- jsou jednoduše vykreslovány závislosti koeficientů odraznosti a propustnosti a odraznosti a propustnosti jako energetických veličin v závislosti na úhlu dopadu elektromagnetických vln na rozhraní dvou homogenních izotropních dielektrik
- pomocí animací lze sledovat změny těchto závislostí na parametrech, jako jsou např. indexy lomu prostředí
- v animacích jsou zobrazeny změny vykreslovaných veličin v intervalu hodnot indexu lomu hustšího prostředí (od 1.4 do 1.96), dále jsou zde znázorňovány okamžité hodnoty Brewsterova úhlu a mezního úhlu
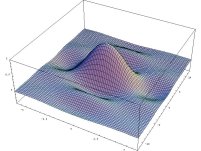
vi) Fraunhoferovy ohybové jevy
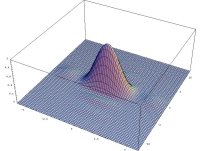
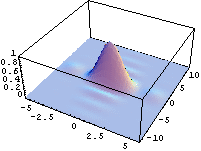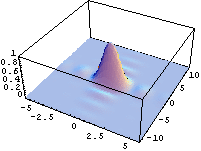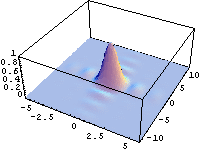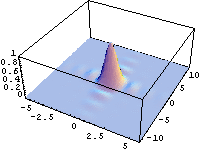
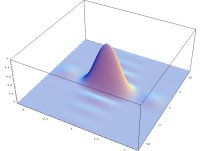
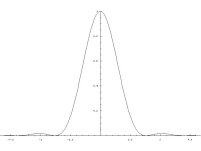
- výpočet a znázornění rozložení intenzity ve Fraunhoferových ohybových jevech
- výsledky jsou znázorněny jak ve formě 3D grafů, tak i např. ve formě tzv. "hustotních" grafů (density plot), kdy je možno jednoduše získat obrázky velmi podobné fotografiím ohybových jevů.
- pomocí animace je možno např. demostrovat změnu šířky hlavního maxima v závislosti na změně rozměrů otvoru
Fraunhoferovy ohybové jevy
|
 obrázek - graf1.jpg  obrázek - graf2.jpg  animace - graf6.gif |
 obrázek - graf5.jpg  obrázek - graf4.jpg  obrázek - grafkruhovyotvor.jpg |
Materiál k teorii elektromagnetického pole v kompletním archivu - elmn.7z (velikost 11,2 MB) nebo elmn.zip (velikost 17,5 MB)
pozn.:
k rozbalení souboru elmn.7z lze použít archivátor WinRar nebo přímo komprimátor 7zip, stáhnout jej lze z domovské stránky projektu http://www.7-zip.org/
Všechny soubory s příponou .nb lze otevřít v prohlížeči MathReader:
